believe me -it's worth it

Frugal nature: Euler and the calculus of variations

i
Frugal nature: Euler and the calculus of variations
by Phil Wilson


Dido and her lover Aeneas

Aeneas tells Dido about the fall of Troy. Baron Pierre-Narcisse Guérin.

Denied by her brother, the killer of her husband, a share of the golden throne of the ancient Phoenician city of Tyre, Dido convinces her brother's servants and some senators to flee with her across the sea in boats laden with her husband's gold. After a brief stop in Cyprus to pick up a priest and to "acquire" some wives for the men, the boats continue, rather lower in the water, to the Northern coast of Africa. Landing in modern-day Tunisia, Dido requests a small piece of land to rest on, only for a little while, and only as big as could be surrounded by the leather from a single oxhide. "Sure," the locals probably thought, "We can spare such a trifling bit of land."

Neither history nor legend recalls who wielded the knife, but Dido arranged to have the oxhide cut into very thin strips, which tied together were long enough to surround an entire hill. "That'll do nicely," we can imagine Dido thinking, and I'm sure we can all make a pretty good guess as to what the locals were thinking too. The city of Carthage was founded on this hill named Byrsa ("Oxhide"), and the civilisation it fostered became a major centre of culture and trade for 668 years until its destruction in 146 BCE, although the city lives on as a suburb of Tunis.

Celebrated in perishable poems and paintings, Queen Dido has been given more durable fame by mathematicians, who have named the following problem after her:

Given a choice from all planar closed curves [curves in the plane whose endpoints join up] of equal perimeter, which encloses the maximum area?

The Dido, or isoperimetric, problem is an example of a class of problems in which a given quantity (here the enclosed area) is to be maximised. But the Dido problem is also equivalent to asking which of all planar closed curves of fixed area minimises the perimeter, and so is an example of the more general problem of finding an extremal value — a maximum or minimum. Extremising problems have been an obsession among physicists and mathematicians for at least the last 400 years. A first mention comes from much further back: around 1700 years ago Pappus of Alexandria noted that the hexagonal honeycombs of bees hold more honey than squares or triangles would.

Extremising principles exhibit an apparent universality and deductive power that has led many otherwise rational minds to take a few nervous steps backwards and invoke a god or other mystical unifying animistic force to account for them. One such mind belonged to Leonhard Euler, the Swiss mathematician whose 300th anniversary we celebrate this year. This reaction is perhaps less surprising in Euler's case, since he entered the University of Basel at the age of 14 to study theology. Luckily for maths he spent his Saturdays hanging out with the great mathematician Johann Bernoulli.

Bernoulli was great, but Euler was greater, and his lifetime output of over 800 books and papers included the foundations of still-vital research fields today, including fluid dynamics, celestial mechanics, number theory, and topology. Another Plus article this year has documented the colourful life of this father of 13 who would knock out a paper before dinner while dangling a baby on his knee. We will focus on Euler's calculus of variations, a method applicable to solving the entire class of extremising problems.

Extreme answers to tricky questions
The front page of Euler's 1744 book. Image courtesy Posner Collection, Carnegie Mellon University Libraries, Pittsburgh PA, USA.



Mathematicians and scientists had been playing with the ideas which Euler systematised in his 1744 book Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti (A method for finding curved lines enjoying properties of maximum or minimum, or solution of isoperimetric problems in the broadest accepted sense). Indeed, Euler himself first published on this topic in 1732, when he wrote the article De linea brevissima in superficie quacunque duo quaelibet puncta jungente (On the shortest line joining two points on a surface) based on an assignment given to him by Bernoulli — persuasive encouragement to always do your homework. It was in his 1744 book, though, that Euler transformed a set of special cases into a systematic approach to general problems: the calculus of variations was born.

Euler coined the term calculus of variations, or variational calculus, based on the notation of Joseph-Louis Lagrange whose work formalised some of the underlying concepts. In their joint honour, the central equation of the calculus of variations is called the Euler-Lagrange equation. But why call it a calculus at all? What has it to do with the Newton-Leibniz differential calculus we encounter at school?
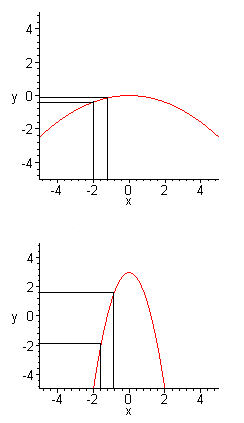
Two graphs of functions.

Figure 1: If the curve is flat, as the one shown on the top, then a small change in x corresponds to a small change in y. The steep curve below has the same change in x corresponding to a larger change in y. To find the slope at a given point, you calculate the limit of the ratios of changes in x and y as the size of the interval on the x-axis tends to zero. At the highest point of both curves — the maximum — the slope is zero.


Differential calculus is concerned with the rates of change of quantities. Take, for example, the slope of a graph representing a function of one independent variable. We might call the variable x and the function y(x). To work out the slope at a given point x, we move a little to the left of x and then a little to the right of x and measure how the value of the function changes from the leftmost position to the rightmost. The ratio of the change in function value to the change in variable value gets closer and closer to the actual slope of the function as the little bit we move to the left and right shrinks to zero. Applying this process to every point x, you end up with the function's derivative, usually written as dy/dx or y'(x).

Differential calculus enables you to find the stationary points of functions, locations at which the slope is zero; these are either extrema (maxima or minima) or inflectional points of the curve. The stationary points are the values of x which satisfy what is called an ordinary differential equation, namely dy/dx=0.


The calculus of variations also deals with rates of change. The difference is that this time you are looking at functions of functions, which are called functionals. As a simple example, think of all the non-self-intersecting curves connecting two given points in the plane. For each curve c, you can work out its length l(c) (if you know your calculus, you'll remember that this is done using integrals). If you want to know how length varies over the different curves, you treat c as a variable and the length l(c) as a function of the variable. But now c isn't as simple as our x above — it's not just a placeholder for a number, but a curve. Mathematically, a curve can be written as a function; the straight line in figure 2, for example, consists of all points with co-ordinates (x,2x). In this example the y coordinate of each point (x,y) on the line is equal to 2x, so we can express the curve as the function
y(x) = 2x. In general the length l(c) is a function of a function — a functional.
The line y = 2x.

Figure 2: The line y = 2x.

The calculus of variations enables you to find stationary points of functionals and the functions at which the extrema occur, the extremising functions. (Mathematically, the process involves finding stationary points of integrals of unknown functions.) In our example, an extremising curve would be one that maximises or minimises curve length.

It turns out that the extremising functions are those which satisfy a an ordinary differential equation, the Euler-Lagrange equation. Euler and Lagrange established the mathematical machinery behind this in a formal and systematic way and in full generality for all extremising problems. Importantly, the new systematic theory allowed for the inclusion of constraints, meaning that a whole swathe of problems in which something must be extremised while something else is kept fixed could be solved. Dido, who maximised the area for a fixed perimeter, would have been proud.


Lazy nature



Euler's foundational 1744 book is one of the first (along with the works of Pierre Louis Maupertuis) to present and discuss the physical principle of least action, indicating a deep — and controversial — connection between the calculus of variations and physics. The principle of least action can be stated informally as "nature is frugal": all physical systems — the orbiting planets, the apple that supposedly fell on Newton's head, the movement of photons — behave in a way that minimises the effort required. The word "effort" here is used in a rather vague sense — the quantity is more properly termed the action of the system. So what is this action, and what (or who, we might once have asked) does the minimising? Why should the universe be run along this parsimonious principle anyway?

Euler formulated a precise definition of the action for a body moving without resistance. Once you know what the action of a particular system is, Euler and Lagrange's calculus of variations becomes a powerful tool for deducing the laws of nature. If you know where and when the body started out and where and when it ended up, then you can use variational calculus to find the path between these endpoints that minimises action. According to the least action principle, this is the path the body must take, so the method should give you information on the fundamental laws governing the motion. If you do the calculations, you'll find out that the well-known equations of motion do indeed pop out in the end. Since Euler's time appropriate actions have been defined for all sorts of physical systems. Euler and Lagrange contributed substantially to this work, but we should also mention William Rowan Hamilton, who built on Euler's work to bring the least action principle to its modern form. Least action principles play an important role in modern physics, including the theory of relativity and, as we shall see, in quantum mechanics.
Maths and god: the limits of knowledge

The principle of least action raises two deep and unanswered issues which bump up against the limits of our knowledge and of what is knowable. It's these that have caused scientists to invoke a god as a default answer, a hypothesis which, arguably, explains nothing at best, and at worst raises more difficult questions than it answers.

The first issue is why our universe should be parsimonious. Stopping short of invoking a god as an explanation, how can we address such an issue? One way would be to ask what a universe without a least action principle would be like. Could life arise? Could explanatory theories and accurate predictions be made in such a universe? This possible line of reasoning invokes the anthropic principle, which states that naturally the universe seems explainable and cosy for life, since, if it were not, we wouldn't be around to argue about it. Unfortunately, this answer leaves our current science behind, because there is as yet no way we can test whether it is true or not.
Sun shining through clouds

Why do sunbeams travel along optimal paths?

The second issue is how the universe achieves being parsimonious. The principle of least action and variational calculus seem to suggest that the behaviour of everything in the universe is dictated by the future. A particle can only take a path of least action if it "knows" where it is going to end up — different endpoints will yield different paths. But how can that be the way the universe actually operates? How can the universe depend on knowing where the system ends up in order to work out how it got there? It doesn't make any sense ... yet the method of variational calculus works. This issue goes beyond the teleological notion that there is a plan or design in the universe. It invokes perfect knowledge of the future for the entire universe — everything is done and dusted and things like free will, morality and scientific endeavour become meaningless.

One possible solution to this problem may lie in a future understanding of how the laws of quantum mechanics — the unbelievably accurate but non-commonsensical theory of the interactions of subatomic particles — give rise to the everyday laws and concepts we see around us. Since we don't operate at the quantum mechanical length scales or time scales, we see only approximations of underlying reality. Our laws may arise from statistical correlations smoothed over innumerable interactions at the smallest scales. There is indeed a least action principle of quantum mechanics and, promisingly, it presents no teleological problems.

Putting aside unresolved philosophical questions, the calculus of variations is a technique of great power used everyday by scientists and mathematicians around the globe to solve real questions posed by the natural, industrial, and biomedical worlds. We will end with an event early in the life of its founder and birthday boy of the year, Leonhard Euler. In 1727, at the age of 20 and before formulating the calculus of variations, Euler caught the world's attention by writing a maths essay (there's hope for me yet) which received an honourable mention in the annual Grand Prix of the Paris Academy of Sciences, certainly the Nobel Prize of the day. Euler's essay was motivated by a real-world problem: how optimally to position the masts on a ship — and this from a man who had never left land-locked Switzerland, nor seen a big sailing ship. He wrote "I did not find it necessary to confirm this theory of mine by experiment because it is derived from the surest and most secure principles of mechanics, so that no doubt whatsoever can be raised on whether or not it be true and takes place in practice." Even after Newton the dangerous idea that mathematics could faithfully reproduce reality was still startling. To this day the implications of this idea are changing the world.
calculus Euler euler year anthropic principle variational calculus least action principle mathematics and religion derivative differentiation pendulum

About the author
Phil Wilson

Phil Wilson is a lecturer in mathematics at the University of Canterbury, New Zealand. He applies mathematics to the biological, medical, industrial, and natural worlds. You can read more of his inspired writing on his blog.
Download PDF version |

http://plus.maths.org/issue44/features/wilson/index.html

http://tinyurl.com/3fxgcb

told you so

Do We Live in a Giant Cosmic Bubble? | LiveScience

Do We Live in a Giant Cosmic Bubble?

By Clara Moskowitz, Staff Writer

posted: 30 September 2008 06:48 am ET

If the notion of dark energy sounds improbable, get ready for an even more outlandish suggestion.

Earth may be trapped in an abnormal bubble of space-time that is particularly void of matter. Scientists say this condition could account for the apparent acceleration of the universe's expansion, for which dark energy currently is the leading explanation.

Dark energy is the name given to the hypothetical force that could be drawing all the stuff in the universe outward at an ever-increasing rate. Current thinking is that 74 percent of the universe could be made up of this exotic dark energy, with another 21 percent being dark matter, and normal matter comprising the remaining 5 percent.

Until now, there has been no good way to choose between dark energy or the void explanation, but a new study outlines a potential test of the bubble scenario.

If we were in an unusually sparse area of the universe, then things could look farther away than they really are and there would be no need to rely on dark energy as an explanation for certain astronomical observations.

"If we lived in a very large under-density, then the space-time itself wouldn't be accelerating," said researcher Timothy Clifton of Oxford University in England. "It would just be that the observations, if interpreted in the usual way, would look like they were."

Scientists first detected the acceleration by noting that distant supernovae seemed to be moving away from us faster than they should be. One type of supernova (called Type Ia) is a useful distance indicator, because the explosions always have the same intrinsic brightness. Since light gets dimmer the farther it travels, that means that when the supernovae appear faint to us, they are far away, and when they appear bright, they are closer in.

But if we happened to be in a portion of the universe with less matter in it than normal, then the space-time around us would be different than it is outside, because matter warps space-time. Light travelling from supernovae outside our bubble would appear dimmer, because the light would diverge more than we would expect once it got inside our void.

One problem with the void idea, though, is that it negates a principle that has reined in astronomy for more than 450 years: namely, that our place in the universe isn't special. When Nicholas Copernicus argued that it made much more sense for the Earth to be revolving around the sun than vice versa, it revolutionized science. Since then, most theories have to pass the Copernican test. If they require our planet to be unique, or our position to be exalted, the ideas often seem unlikely.

"This idea that we live in a void would really be a statement that we live in a special place," Clifton told SPACE.com. "The regular cosmological model is based on the idea that where we live is a typical place in the universe. This would be a contradiction to the Copernican principle."

Clifton, along with Oxford researchers Pedro G. Ferreira and Kate Land, say that in coming years we may be able to distinguish between dark energy and the void. They point to the upcoming Joint Dark Energy Mission, planned by NASA and the U.S. Department of Energy to launch in 2014 or 2015. The satellite aims to measure the expansion of the universe precisely by observing about 2,300 supernovae.

The scientists suggest that by looking at a large number of supernovae in a certain region of the universe, they should be able to tell whether the objects are really accelerating away, or if their light is merely being distorted in a void.

The new study will be detailed in an upcoming issue of the journal Physical Review Letters.

but can it detect bs?

Invention: Universal detector - tech - 26 September 2008 - New Scientist Tech

Invention: Universal detector

* 16:51 26 September 2008
* NewScientist.com news service
* Justin Mullins

Advertisement

Zap a metal with light and the electrons on the surface ripple into waves – known as plasmons – which emit light of their own. The frequency of that light reflects the electronic nature of the surface and is highly sensitive to contamination.

Kevin Tetz and colleagues in the Ultrafast and Nanoscale Optics Group at the University of California, San Diego, have designed a system to exploit that to test for any surface contamination on the surface of, well, anything.

Their idea uses a thin layer of metal drilled with nanoscale holes, laid onto the surface being tested. When the perforated plate is zapped with laser light, the surface plasmons that form emit light with a frequency related to the materials touching the plate. A sensitive light detector is needed to measure the frequency of light given off.

The team says devices using this approach can be small and portable, will work on very low power, and could detect everything from explosives to bacteria. All that needs to be done now is build a system able to decode the light signatures.

Read the full universal detector patent application

Hybrid Nanoparticles Image and Treat Tumors

Print the story

Hybrid Nanoparticles Image and Treat Tumors

(PhysOrg.com) -- By combining a magnetic nanoparticle, a fluorescent quantum dot, and an anticancer drug within a lipid-based nanoparticle, a multi-institutional research team headed by members of the National Cancer Institute’s (NCI) Alliance for Nanotechnology in Cancer has created a single agent that can image and treat tumors. In addition, this new nanoparticle is able to avoid detection by the immune system, enabling the particle to remain in the body for extended periods of time.

“The idea involves encapsulating imaging agents and drugs into a protective ‘mothership’ that evades the natural processes that normally would remove these payloads if they were unprotected,” said Michael Sailor, Ph.D., an Alliance member at the University of California, San Diego, who led this research effort. Other Alliance members who participated in this study include Sangeeta Bhatia, M.D., Ph.D., Massachusetts Institute of Technology, and Erkki Ruoslahti, M.D., Ph.D., Burnham Institute for Medical Research at the University of California, Santa Barbara. The researchers published the results of their work in the journal Angewandte Chemie International Edition.

“Many drugs look promising in the laboratory but fail in humans because they do not reach the diseased tissue in time or at concentrations high enough to be effective,” added Dr. Bhatia. “These drugs don’t have the capability to avoid the body’s natural defenses or to discriminate their intended targets from healthy tissues. In addition, we lack the tools to detect diseases such as cancer at the earliest stages of development, when therapies can be most effective.”

The researchers designed the hull of their motherships to evade detection by constructing them of lipids modified with poly(ethylene glycol) (PEG). The researchers also designed the material of the hull to be strong enough to prevent accidental release of the mothership’s cargo while circulating through the bloodstream. Tethered to the surface of the hull is a protein called F3, a molecule that sticks to cancer cells. Prepared in Dr. Ruoslahti’s laboratory, F3 was engineered to specifically home in on tumor cell surfaces and then transport itself into their nuclei.

The researchers loaded their mothership nanoparticles with three payloads before injecting them in mice. Two types of nanoparticles, superparamagnetic iron oxide and fluorescent quantum dots, were placed in the ship’s cargo hold, along with the anticancer drug doxorubicin. The iron oxide nanoparticles allow the ships to show up in a magnetic resonance imaging (MRI) scan, and the quantum dots can be seen with another type of imaging tool, a fluorescence scanner.

“The fluorescence image provides higher resolution than MRI,” said Dr. Sailor. “One can imagine a surgeon identifying the specific location of a tumor in the body before surgery with an MRI scan, then using fluorescence imaging to find and remove all parts of the tumor during the operation.”

To its surprise, the team found that a single mothership can carry multiple iron oxide nanoparticles, which increases their brightness in the MRI image. “The ability of these nanostructures to carry more than one superparamagnetic nanoparticle makes them easier to see by MRI, which should translate to earlier detection of smaller tumors,” said Dr. Sailor. “The fact that the ships can carry very dissimilar payloads—a magnetic nanoparticle, a fluorescent quantum dot, and a small molecule drug—was a real surprise.”

This work, which is detailed in the paper “Micellar Hybrid Nanoparticles for Simultaneous Magnetofluorescent Imaging and Drug Delivery,” was supported by the NCI Alliance for Nanotechnology in Cancer. (http://dx.doi.org/doi:10.1002/anie.200801810)

Provided by National Cancer Institute




This news is brought to you by PhysOrg.com

It's nothing a case of beer won't fix...

Forget black holes, could the LHC trigger a “Bose supernova”?

Forget black holes, could the LHC trigger a “Bose supernova”?
September 29th, 2008 | by KFC |

lhc-higgs.jpg

The fellas at CERN have gone to great lengths to reassure us all that they won’t destroy the planet (who says physicists are cold hearted?).

The worry was that the collision of particles at the LHC’s high energies could create a black hole that would swallow the planet. We appear to be safe on that score but it turns out there’s another way in which some people think the LHC could cause a major explosion.

The worry this time is about Bose Einstein Condensates, lumps of matter so cold that their constituents occupy the lowest possible quantum state.

Physicists have been fiddling with BECs since the early 1990s and have become quite good at manipulating them with magnetic fields.

One thing they’ve found is that it is possible to switch the force between atoms in certain kinds of BECs from positive to negative and back using a magnetic field, a phenomenon known as a Feschbach resonance.

But get this: in 2001, Elizabeth Donley and buddies at JILA in Boulder, Colorado, caused a BEC to explode by switching the forces like. These explosions have since become known as Bose supernovas.

Nobody is exactly sure how these explosions proceed which is a tad worrying for the following reason: some clever clogs has pointed out that superfluid helium is a BEC and that the LHC is swimming in 700,000 litres of the stuff. Not only that but the entire thing is bathed in some of the most powerful magnetic fields on the planet.

So is the LHC a timebomb waiting to go off? Not according to Malcolm Fairbairn and Bob McElrath at CERN who have filled the back of a few envelopes in calculating that we’re still safe. To be doubly sure, they also checked that no other superfluid helium facilities have mysteriously blown themselves to kingdom come.

“We conclude that that there is no physics whatsoever which suggests that Helium could undergo
any kind of unforeseen catastrophic explosion,” they say.

That’s comforting and impressive. Ruling out foreseen catastrophies is certainly useful but the ability to rule out unforeseen ones is truly amazing.

Ref: arxiv.org/abs/0809.4004: There is no Explosion Risk Associated with Superfluid Helium in the LHC Cooling System

financial phi

How Fractals Can Explain What's Wrong with Wall Street: Scientific American

Editor's Note: This story was originally published in the February 1999 edition of Scientific American. We are posting it in light of recent news involving Lehman Brothers and Merrill Lynch.

Individual investors and professional stock and currency traders know better than ever that prices quoted in any financial market often change with heart-stopping swiftness. Fortunes are made and lost in sudden bursts of activity when the market seems to speed up and the volatility soars. Last September, for instance, the stock for Alcatel, a French telecommunications equipment manufacturer, dropped about 40 percent one day and fell another 6 percent over the next few days. In a reversal, the stock shot up 10 percent on the fourth day.

The classical financial models used for most of this century predict that such precipitous events should never happen. A cornerstone of finance is modern portfolio theory, which tries to maximize returns for a given level of risk. The mathematics underlying portfolio theory handles extreme situations with benign neglect: it regards large market shifts as too unlikely to matter or as impossible to take into account. It is true that portfolio theory may account for what occurs 95 percent of the time in the market. But the picture it presents does not reflect reality, if one agrees that major events are part of the remaining 5 percent. An inescapable analogy is that of a sailor at sea. If the weather is moderate 95 percent of the time, can the mariner afford to ignore the possibility of a typhoon?

The risk-reducing formulas behind portfolio theory rely on a number of demanding and ultimately unfounded premises. First, they suggest that price changes are statistically independent of one another: for example, that today’s price has no influence on the changes between the current price and tomorrow’s. As a result, predictions of future market movements become impossible. The second presumption is that all price changes are distributed in a pattern that conforms to the standard bell curve. The width of the bell shape (as measured by its sigma, or standard deviation) depicts how far price changes diverge from the mean; events at the extremes are considered extremely rare. Typhoons are, in effect, defined out of existence.

Do financial data neatly conform to such assumptions? Of course, they never do. Charts of stock or currency changes over time do reveal a constant background of small up and down price movements—but not as uniform as one would expect if price changes fit the bell curve. These patterns, however, constitute only one aspect of the graph. A substantial number of sudden large changes—spikes on the chart that shoot up and down as with the Alcatel stock—stand out from the background of more moderate perturbations. Moreover, the magnitude of price movements (both large and small) may remain roughly constant for a year, and then suddenly the variability may increase for an extended period. Big price jumps become more common as the turbulence of the market grows—clusters of them appear on the chart.

According to portfolio theory, the probability of these large fluctuations would be a few millionths of a millionth of a millionth of a millionth. (The fluctuations are greater than 10 standard deviations.) But in fact, one observes spikes on a regular basis—as often as every month—and their probability amounts to a few hundredths. Granted, the bell curve is often described as normal—or, more precisely, as the normal distribution. But should financial markets then be described as abnormal? Of course not—they are what they are, and it is portfolio theory that is flawed.

Modern portfolio theory poses a danger to those who believe in it too strongly and is a powerful challenge for the theoretician. Though sometimes acknowledging faults in the present body of thinking, its adherents suggest that no other premises can be handled through mathematical modeling. This contention leads to the question of whether a rigorous quantitative description of at least some features of major financial upheavals can be developed. The bearish answer is that large market swings are anomalies, individual “acts of God” that present no conceivable regularity. Revisionists correct the questionable premises of modern portfolio theory through small fixes that lack any guiding principle and do not improve matters sufficiently. My own work—carried out over many years— takes a very different and decidedly bullish position.

get down with your funky self

Why do we like to dance--And move to the beat?: Scientific American

dance

THE THRILL OF TANGO:

Scientists believe that dancing combines two of our greatest pleasures: movement and music.
© ISTOCKPHOTO/Guillermo Perales Gonzalez

Many things stimulate our brains' reward centers, among them, coordinated movements. Consider the thrill some get from watching choreographed fight or car chase scenes in action movies. What about the enjoyment spectators get when watching sports or actually riding on a roller coaster or in a fast car?

Scientists aren't sure why we like movement so much, but there's certainly a lot of anecdotal evidence to suggest we get a pretty big kick out of it. Maybe synchronizing music, which many studies have shown is pleasing to both the ear and brain, and movement—in essence, dance—may constitute a pleasure double play.

Music is known to stimulate pleasure and reward areas like the orbitofrontal cortex, located directly behind one's eyes, as well as a midbrain region called the ventral striatum. In particular, the amount of activation in these areas matches up with how much we enjoy the tunes. In addition, music activates the cerebellum, at the base of the brain, which is involved in the coordination and timing of movement.

So, why is dance pleasurable?

First, people speculate that music was created through rhythmic movement—think: tapping your foot. Second, some reward-related areas in the brain are connected with motor areas. Third, mounting evidence suggests that we are sensitive and attuned to the movements of others' bodies, because similar brain regions are activated when certain movements are both made and observed. For example, the motor regions of professional dancers' brains show more activation when they watch other dancers compared with people who don't dance.

This kind of finding has led to a great deal of speculation with respect to mirror neurons—cells found in the cortex, the brain's central processing unit, that activate when a person is performing an action as well as watching someone else do it. Increasing evidence suggests that sensory experiences are also motor experiences. Music and dance may just be particularly pleasurable activators of these sensory and motor circuits. So, if you're watching someone dance, your brain's movement areas activate; unconsciously, you are planning and predicting how a dancer would move based on what you would do.

That may lead to the pleasure we get from seeing someone execute a movement with expert skill—that is seeing an action that your own motor system cannot predict via an internal simulation. This prediction error may be rewarding in some way.

So, if that evidence indicates that humans like watching others in motion (and being in motion themselves), adding music to the mix may be a pinnacle of reward.

Music, in fact, can actually refine your movement skills by improving your timing, coordination and rhythm. Take the Brazilian folk art, Capoeira—which could be a dance masquerading as a martial art or vice versa. Many of the moves in that fighting style are choreographed, taught and practiced, along with music, making the participants more adept—and giving them the pleasure from the music as well as from performing the movement.

Adding music in this context may cross the thin line between a killing machine and a dancing machine.

reboot yourself

Cell 'rebooting' technique sidesteps risks : Nature News

Cell 'rebooting' technique sidesteps risks

Virus reprograms cells without disrupting genome.

Erika Check Hayden
stem cellA pluripotent stem cells induced by transient gene delivery.Mathias Stadtfeld and Konrad Hochedlinger

Scientists today announce a major advance in a technology for engineering cells with broad regenerative powers.

Writing in Science1, a team led by biologist Konrad Hochedlinger of Harvard Medical School in Boston, Massachusetts, describes how it transformed mouse tail and liver cells into an embryonic-like state. And unlike other scientists who had previously made such 'induced pluripotent stem cells', or iPS cells, Hochedlinger's team did not use a virus that integrates itself into a cell's genome to 'reboot' the cells. Instead, the team used an adenovirus, which keeps out of a cell's own DNA, avoiding the potential for serious side-effects such as cancer, which might result from viral disruption of a cell's DNA.

The work brings the science of iPS cells one step closer to clinical reality. But it also answers some key biological questions about the cells: "This is a potentially exciting advance, since it gets around the dangers of viral integration into the genome," says Martin Pera, director of the University of Southern California's Institute for Stem Cell and Regenerative Medicine in Los Angeles.
Tailor-made tissues

Scientists are excited about iPS cells because they can theoretically be made from any of an individual's cells, and might therefore be used to tailor-make tissues that match a patient. They are also being used for the study of disease, and avoid the ethical and practical issues surrounding the use of embryonic stem (ES) cells harvested from blastocysts, the hollow balls of cells that form during the early stages of human development . They are also much more readily available than human eggs, which are also being used in one technique to try to reprogram adult cells.

However, many questions remain about the adenovirally reprogramed cells. Some have claimed that the study eliminates the need for work on human ES cells, but Hochedlinger disagrees: "It's much too early to say that — at this point we clearly still need ES cells," he said.

The issue has been a contentious one in the US presidential campaign. Barack Obama has said that iPS cells do not eliminate the need for ES cell research. John McCain's stance has been more vague, while his running mate, Sarah Palin, opposes ES cell work (see 'US election: Questioning the candidates'). Yet Hochedlinger points out that he has not been able to use his technique to reprogram human cells yet, and that even if his lab was able to do so, researchers still do not know whether iPS cells share all of ES cells' powers.

"It is unclear to what extent ES cells and iPS cells are really equivalent to each other, and showing this will require much more work," says Hochedlinger.

yes. it is nature's way...

Sexed robots

walking the walk

Observers of Walking Figures See Men Advancing, Women in Retreat: Scientific American Podcast

One signature detail we use when we recognize people we know—one that is often overlooked—is their walk. Past studies show that we can discern gender, mood, personality traits by just watching animated simple point-figures…meaning, points of light marking joint positions on amblers, such as knees, elbows, hips, etc.

A group from the Southern Cross University in Australia published a fascinating result in the journal Current Biology, after they manipulated the light points of walkers, making figures appear more feminine or masculine.

If they made the point-form body appear male, subjects perceived that figure as walking toward them—regardless of its actual direction. If the walker seemed female, the subjects reported it was walking away from them.

Curiously, gender-neutral figures tended to appear to be moving toward the viewer. "It was only when walkers had characteristics consistent with being female did the observers begin to perceive them more often as facing away," the researchers reported.

Further, even when the researchers included perspective cues that enhance a stroller's directionality, they found subjects saw males as coming toward them more than half the time, and nearly always viewed females as in retreat.

The researchers speculate that these misperceptions may signal deeper evolutionary factors: "…a male figure that is otherwise ambiguous might best be perceived as approaching to allow the observer to prepare to flee or fight. Similarly…especially for infants, the departure of females might signal a need to act…"

Hm. Not sure, but that’s the thing in science… fascinating proven results are often left waiting for their counterpart explanations to catch up.

- Christie Nicholson

shaken virus syndrome

New Way to Kill Viruses: Shake Them to Death | LiveScience

New Way to Kill Viruses: Shake Them to Death

By Michael Schirber, Special to LiveScience



Scientists may one day be able to destroy viruses in the same way that opera singers presumably shatter wine glasses. New research mathematically determined the frequencies at which simple viruses could be shaken to death.

"The capsid of a virus is something like the shell of a turtle," said physicist Otto Sankey of Arizona State University. "If the shell can be compromised [by mechanical vibrations], the virus can be inactivated."

Recent experimental evidence has shown that laser pulses tuned to the right frequency can kill certain viruses. However, locating these so-called resonant frequencies is a bit of trial and error.

"Experiments must just try a wide variety of conditions and hope that conditions are found that can lead to success," Sankey told LiveScience.

To expedite this search, Sankey and his student Eric Dykeman have developed a way to calculate the vibrational motion of every atom in a virus shell. From this, they can determine the lowest resonant frequencies.

As an example of their technique, the team modeled the satellite tobacco necrosis virus and found this small virus resonates strongly around 60 Gigahertz (where one Gigahertz is a billion cycles per second), as reported in the Jan. 14 issue of Physical Review Letters.

A virus' death knell

All objects have resonant frequencies at which they naturally oscillate. Pluck a guitar string and it will vibrate at a resonant frequency.

But resonating can get out of control. A famous example is the Tacoma Narrows Bridge, which warped and finally collapsed in 1940 due to a wind that rocked the bridge back and forth at one of its resonant frequencies.

Viruses are susceptible to the same kind of mechanical excitation. An experimental group led by K. T. Tsen from Arizona State University have recently shown that pulses of laser light can induce destructive vibrations in virus shells.

"The idea is that the time that the pulse is on is about a quarter of a period of a vibration," Sankey said. "Like pushing a child on a swing from rest, one impulsive push gets the virus shaking."

It is difficult to calculate what sort of push will kill a virus, since there can be millions of atoms in its shell structure. A direct computation of each atom's movements would take several hundred thousand Gigabytes of computer memory, Sankey explained.

He and Dykeman have found a method to calculate the resonant frequencies with much less memory.

In practice

The team plans to use their technique to study other, more complicated viruses. However, it is still a long way from using this to neutralize the viruses in infected people.

One challenge is that laser light cannot penetrate the skin very deeply. But Sankey imagines that a patient might be hooked up to a dialysis-like machine that cycles blood through a tube where it can be hit with a laser. Or perhaps, ultrasound can be used instead of lasers.

These treatments would presumably be safer for patients than many antiviral drugs that can have terrible side-effects. Normal cells should not be affected by the virus-killing lasers or sound waves because they have resonant frequencies much lower than those of viruses, Sankey said.

Moreover, it is unlikely that viruses will develop resistance to mechanical shaking, as they do to drugs.

"This is such a new field, and there are so few experiments, that the science has not yet had sufficient time to prove itself," Sankey said. "We remain hopeful but remain skeptical at the same time."

the incredible lightness of gravity

A U.S. graduate student won second place in a "Greener Gadgets Conference" competition inventing a floor lamp powered by gravity.

Clay Moulton of Springfield, Va., who received his master's of science degree last year from Virginia Tech, created the lamp as a part of his master's thesis. The LED lamp, named Gravia, is an acrylic column a little more than 4 feet high. The entire column glows when activated by electricity generated by the slow, silent fall of a mass that spins a rotor.

The light output of 600-800 lumens lasts about four hours.

To "turn on" the lamp, the user moves weights from the bottom to the top of the lamp and into a mass sled near the top. The sled begins its gentle glide down and, within a few seconds, the LEDs are illuminated.

"It's more complicated than flipping a switch," said Moulton, "but can be an acceptable, even enjoyable routine, like winding a beautiful clock or making good coffee."

Moulton estimates Gravia's mechanisms will last more than 200 years.

A patent is pending on the Gravia lamp.

this is your brain on poverty

The Stress of Poverty Changes the Brain Blogs Scientific American Community

mysterious crystal

Huge crystal baffles chemists

Molecular cluster defies accurate analysis.

Katharine Sanderson

A giant molecular bauble, by far the largest single-molecule metal-cluster ever made, is confounding chemists. Involving almost 500 silver atoms, the crystals are so large and complex that their creators cannot figure out their structure.
Each of the 30 crystals made by Dieter Fenske of the University of Karlsruhe in Germany and his colleagues is thought to contain molecules with 490 silver atoms linked by 188 sulphur atoms and 114 organic groups, Ag₄₉₀S₁₈₈(StC₅H₁₁)₁₁₄. “This is an idealized structure” based on energy calculations, explains Fenske, who published the structure this month (C. E. Anson et al. Angew. Chem. Int. Edn doi:10.1002/anie.200704249 2008).

Atomic mess: the exact structure of this giant crystal may prove impossible to determine.

“With structures that size you are pushing the crystallography technique right to its limit,” says chemist Paul Raithby at the University of Bath, UK. Yet, he adds: “As far as crystallography and mass spectrometry can prove anything, this structure is as definitively proved as you could get.”
Fenske's molecules, described as 'clusters', produce molecules that are about 3 nanometres in diameter. The crystals have a well-defined outer 'shell' that is possible, though not simple, to characterize using X-ray diffraction.
But delve beneath the crystals' outer shell and things get a lot more complicated. Rather than the regular structure seen in a typical crystal, Fenske's clusters contain disorder: a void, filled by silver and sulphur atoms linked together in haphazard disarray. Molecules of silver sulphide (Ag₂S) can be arranged in a number of different geometries, including cubic, octahedral or dodecahedral. The disorder inside Fenske's cluster is so great that he can't tell what the geometry is in any of his samples. He describes the interior as looking “molten”.
The crystals have been tricky to define in more than one way: even though they grow in a crystalline way, the disordered core causes a problem. “If the interior of the particles is 'mobile' then they are not crystals,” says Frank Leusen, a crystallographer at Bradford University, UK. And are they molecules? Some say yes, others are not so sure. “These systems are at the boundary between molecular chemistry and bulk materials chemistry,” says Raithby. “I am at a bit of a loss finding an appropriate term,” adds Leusen.
Because of their huge size, Fenske's clusters may have characteristics that transcend the limits of molecular chemistry and enter the realm of macroscopic particles. For example, they may have interesting electrical properties.
The sheer size and complexity of the clusters mean that their internal structure cannot be revealed using X-ray diffraction. The technique uses X-rays that are reflected off the atoms in a rotating crystal, creating patterns of spots. These spots are converted into a map of the electron density around the atoms, and eventually the molecule's structure is calculated. But with larger molecules the number of spots increases, the spots get closer together and can even overlap. Also the intensity of each spot decreases as molecules get bigger.
Fenske instead calculated likely arrangements for the different internal geometries that Ag₂S could adopt within the known molecular mass. The most tightly packed arrangement, Fenske calculated, involves 490 silver atoms, making it by far the largest cluster reported.

ADVERTISEMENT

“The research in this paper is spectacular,” says Bill Clegg, a crystallographer at Newcastle University, UK.

But Fenske is not stopping there. In the same mixture that produced the black crystals he thinks he has a cluster that contains 800 silver atoms, the structure of which he is grappling with at the moment. “I'm pretty sure we can get larger particles,” he says.
.

***************
"you have found the answer when you accept life for what it is, that the universe is unfathomable and everything is unobtainable."

weird water

Weird water: Discovery challenges long-held beliefs about water's special properties Beyond its role as the elixir of all life, water is a very unusual substance: Scientists have long marveled over counter-intuitive properties that set water apart from other solids and liquids commonly found in nature. The simple fact that water expands when it freezes -- an effect known to anyone whose plumbing has burst in winter -- is just the beginning of a long list of special characteristics. (Most liquids contract when they freeze.) That is why chemical engineer Pablo Debenedetti and collaborators at three other institutions were surprised to find a highly simplified model molecule that behaves in much the same way as water, a discovery that upends long-held beliefs about what makes water so special. “The conventional wisdom is that water is unique,” said Debenedetti, the Class of 1950 Professor in Engineering and Applied Science. “And here we have a very simple model that displays behaviors that are very hard to get in anything but water. It forces you to rethink what is unique about water.” While their water imitator is hypothetical -- it was created with computer software that is commonly used for simulating interactions between molecules -- the researchers’ discovery may ultimately have implications for industrial or pharmaceutical research. “I would be very interested to see if experimentalists could create colloids (small particles suspended in liquid) that exhibit the water-like properties we observed in our simulations,” Debenedetti said. Such laboratory creations might be useful in controlling the self-assembly of complex biomolecules or detergents and other surfactants. . More fundamentally, the research raises questions about why oil and water don’t mix, because the simulated molecule repels oil as water does, but without the delicate interactions between hydrogen and oxygen that are thought to give water much of its special behavior. The researchers published their findings Dec. 12 in the Proceedings of the National Academy of Sciences. The team also included lead author Sergey V. Buldyrev of Yeshiva University, Pradeep Kumar and H. Eugene Stanley of Boston University, and Peter J. Rossky of the University of Texas. The research was funded by the National Science Foundation through a grant shared by Debenedetti, Rossky and Stanley. The discovery builds on an earlier advance by the same researchers. It had previously been shown that simple molecules can show some water-like features. In 2006, the collaborators published a paper showing that they could induce water-like peculiarities by adjusting the distance at which pairs of particles start to repel each other. Like water, their simulated substance expanded when cooled and became more slippery when pressurized. That finding led them to investigate more closely. They decided to look at how their simulated molecule acts as a solvent -- that is, how it behaves when other materials are dissolved into it -- because water’s behavior as a solvent is also unique. In their current paper, they simulated the introduction of oily materials into their imitator and showed that it had the same oil-water repulsion as real water across a range of temperatures. They also simulated dissolving oily polymers into their substance and, again, found water-like behavior. In particular, the polymers swelled not only when the “water” was heated, but also when it was super-cooled, which is one defining characteristic of real water. Proteins with oily interiors also behave in this way. In real water, these special behaviors are thought to arise from water’s structure -- two hydrogen atoms attached to an oxygen atom. The arrangement of electrical charges causes water molecules to twist and stick to each other in complex ways. To create their simulation, the researchers ignored these complexities. They specified just two properties: the distance at which two converging particles start to repel each other and the distance at which they actually collide like billiard balls. Their particles could be made of anything -- plastic beads, for example -- and so long as the ratio between these two distances was correct (7:4), then they would display many of the same characteristics as water. “This model is so simple it is almost a caricature,” Debenedetti said. “And yet it has these very special properties. To show that you can have oil-water repulsion without hydrogen bonds is quite interesting.” Debenedetti noted that their particles differ from water in key aspects. When it freezes, for example, the crystals do not look anything like ice. For that reason, the research should not be viewed as leading toward a “water substitute.” As a next step, Debenedetti said he would like to see if experimentalists could create particles that have the same simple specifications as their model and see if their behavior matches the computer simulation. Source: Princeton University